1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
| import matplotlib.path as mpath
import matplotlib.patches as mpatches
import matplotlib.pyplot as plt
import numpy as np
from scipy import stats
def random_dir():
direction = {1: (0, 1), 2: (0, -1), 3: (1, 0), 4: (-1, 0)}
xk = (1, 2, 3, 4)
pk = (0.25, 0.25, 0.25, 0.25)
unifdb = stats.rv_discrete(name='unifdb', values=(xk, pk))
return direction[unifdb.rvs()]
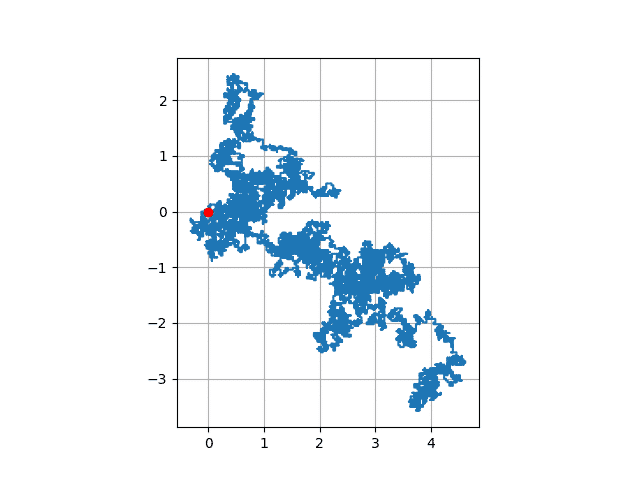
def random_walk(n, starting=(0, 0)):
fig, ax = plt.subplots()
Path = mpath.Path
path_data = [(Path.MOVETO, starting)]
l = [starting]
for k in range(n):
l.append(random_dir())
s = tuple([sum(x) for x in zip(*l)])
l = [s]
path_data.append((Path.CURVE4, s))
codes, verts = zip(*path_data)
path = mpath.Path(verts, codes)
x, y = zip(*path.vertices)
line = ax.plot(x, y)
ax.plot(starting[0], starting[1], 'ro')
ax.grid()
plt.gca().set_aspect('equal', adjustable='box')
plt.show()
def normalized_random_walk(N, t, starting=(0, 0)):
fig, ax = plt.subplots()
Path = mpath.Path
path_data = [(Path.MOVETO, starting)]
n = int(N * t)
l = [starting]
for k in range(n):
l.append(tuple(1.0 / np.sqrt(N) * x for x in random_dir()))
s = tuple(sum(x) for x in zip(*l))
l = [s]
path_data.append((Path.CURVE4, s))
l.append(tuple((N * t - n) / np.sqrt(N) * x for x in random_dir()))
path_data.append((Path.CURVE4, tuple(sum(x) for x in zip(*l))))
codes, verts = zip(*path_data)
path = mpath.Path(verts, codes)
x, y = zip(*path.vertices)
line = ax.plot(x, y)
ax.plot(starting[0], starting[1], 'ro')
ax.grid()
plt.gca().set_aspect('equal', adjustable='box')
plt.show()
|